The slant height of a cone should not be confused with the height of a cone. Slant height is the distance from the top of a cone, down the side to the edge of the circular base. Slant height is calculated as \(\sqrt\), where \(r\) represents the radius of the circular base, and \(h\) represents the height, or altitude, of the cone.
The surface area of a cone is the sum of the lateral surface area and the base surface area. If you know the radius of the base and the slant height of the cone, you can easily find the total surface area using a standard formula. Sometimes, however, you might have the radius and some other measurement, such as the height or volume of the cone. In these instances, you can use the Pythagorean Theorem and the volume formula to derive the slant height, and thus the surface area of the cone. To calculate the slant height of either a cone or a pyramid, you need to imagine that you can look inside of the figure. First, we cut down through the cone from vertex point A to segment BC to get two halves.
The cut surface of either half is now in the shape of an isosceles triangle, which is a triangle with two sides that are the same length. Those two sides were the slant height of the cone. We now have triangle ABC, where sides AB and AC have the same length. A cone folded flat forms a sector of a larger circle.Imagine a cone without its base, made out of paper.
You then roll it out so it lies flat on a table. You will get a shape like the one in the diagram above. It is a part of a larger circle, whose radius is equal to the slant height of the cone. The arc length of the sector is equivalent to the circumference of the cone base.
In the video lesson, we learned how to find the slant height of a cone or pyramid when we know the altitude and information about the base. The same formula for slant height can be manipulated to find the altitude, the radius of the base , or half the side length of the base . The red segment DM measured 8 inches and that same segment is one side of the triangle. The purple segment DY was the slant height of the pyramid, and it forms the hypotenuse of the triangle. DY is the length we are trying to calculate, so we will give it the variable c. Our traffic cone is a little different from the geometric shape called a cone.
In geometry, the base of a cone is only a circle that does not extend beyond the opening of the cone. The point of a cone in geometry is called the vertex point. The slant height and the altitude always meet at that vertex point in a cone.
On the traffic cone, the two segments did not meet because the tip is flat and does not come to one point. So, to solve the volume and surface area equations, we'd simply plug a cone's measurements into the respective variables. It's the total area of the surface of a shape. Think of volume as the amount of liquid that you could fill an object with, and think of surface area as how much paper you could wrap over that object. But the trick is to figure out how to design a 2-D net for the cone.
Did you know that the 2-D net for a cone is a sector of a circle? Here, the circle we are talking about has radius s . So we know the radius of the sector is s, not r.
But the big question is, how big is the angle of the sector? The amount of the circumference of the sector is the same as the whole circumference of the cone's base, namely, 2𝜋r. The distance along the outside of a cone, from the top to the base, is known as the slant height.
A cone is a three dimensional geometric shape with one vertex and a circular base. The line form the centre of the base to the apex is the perpendicular height. Identify the radius of the cone's base circle. If you have the diameter, cut it in half to get the radius.
If you have the slant height and perpendicular height, use the Pythagorean theorem. The "height" of a cone, and the "slant height" of a cone are not the same thing. The height of a cone is considered the vertical height or altitude of the cone. This is the perpendicular distance from the top of the cone down to the center of the circular base.
The slant height of a cone is the distance from the top of the cone, down the side of the cone to the edge of the circular base. Welcome to today's video where we're going to talk about the volume and surface area of a cone. We know that a cone is actually a lot like a pyramid. While a pyramid has a square base that connects to a pointy tip at the opposite end, a cone's base is, instead, a circle.
Enter a value for the radius of the circular base. Remember that the radius is half of the diameter of a circle. You can choose different units of length, depending on the problem or measurement taken. Alternatively, you can enter the circumference of the circular base instead. The slant height of a cone or pyramid is the length of a segment from the vertex point to the base along the outside of the shape.
Let's go through an example where we calculate the length of the slant height of a pyramid. In this example, we are given that the altitude of the pyramid measures 8 inches and each side of the base is 12 inches long. The altitude is the dashed red segment DM and the slant height is the purple segment DY.
How To Find Volume Of A Cone Given Radius And Slant Height Let's consider a traffic cone to help us learn the difference between these two measurements. If you measure the distance along the outside of the cone from the top to the base, that measurement is the slant height. To measure it, you have to place the yardstick at a slant. Figures such as cones and pyramids have two measurements that indicate how tall the figure is. One of these measurements is called the slant height and the other is called the altitude.
Given radius and slant height calculate the height, volume, lateral surface area and total surface area. This online calculator will calculate the various properties of a right circular cone given any 2 known variables. The term "circular" clarifies this shape as a pyramid with a circular cross section. The term "right" means that the vertex of the cone is centered above the base.
Using the term "cone" by itself often commonly means a right circular cone. Assuming you are given the lateral surface area and the slant height, divide the lateral surface area by the product of pi and the slant height. Take the square root of each side of the equation. This will give you the length of the hypotenuse of the right triangle, which is equal to the slant height of the cone.
The formula for the lateral surface area of a cone is the radius multiplied by the slant height multiplied by pi. Enter the height of the cone or the slant height of the cone, depending on which one is known. The height is the perpendicular distance between the cone tip and the center of the circular base.
The slant height is the distance between the tip and the outside edge of the base. This calculator is for a particular type of cone called a right cone . It has a circular base, and the vertex is directly above the center of the base. Therefore, the angle made between the base and an imaginary line between the base and the vertex is 90°, commonly known as a right angle.
Let $\varphi$ denote the angle of the sector of the circle. Find the altitude of a cone whose base diameter is 6 feet and whose slant height is 9 feet. Given height and slant height calculate the radius, volume, lateral surface area and total surface area.
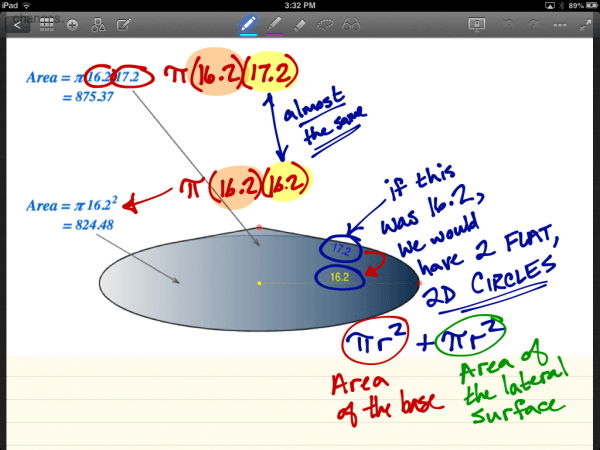
Given radius and height calculate the slant height, volume, lateral surface area and total surface area. The slant height of a pyramid is √[(s/2)² + h²] and the slant height of a cone is √[r² + h²]. The radius is r, the height is h, and the side of the base is s. The lateral area of a cone with radius 4 cm is 60 cm. Surface area of a cone, we divide it into a circular base and the top slanted part. The area of the slanted part gives you the curved surface area.
Total surface area is the sum of this circular base and curved surface areas. This surface area of a cone calculator will help you calculate the surface area of any right cone. In the text below, we will show you the surface area of a cone formula and how to derive it. After using our calculator and reading this article, you'll be super confident about how to find the surface area of a cone.
0 Find the volume of a right circular cone formed by joining the edges of a sector of a circle of radius r cm where the sector angle is 90 degrees. The slant height and the altitude are both sides of a right triangle that can be visualized inside every cone and pyramid. Given slant height and lateral surface area calculate the radius, height, volume, and total surface area. Given height and volume calculate the radius, slant height, lateral surface area and total surface area. Given radius and total surface area calculate the height, slant height, volume and lateral surface area.
Given radius and lateral surface area calculate the height, slant height, volume and total surface area. Given radius and volume calculate the height, slant height, lateral surface area and total surface area. A Cone is a geometric shape formed by having a circle at one end, usually at a base. It consists of all line segments joining to a single point to every point of a two-dimensional figure.
Multiply the slant height times the radius times pi. Again, "exact value" means write pi as pi; otherwise, use 3.14 to get the decimal approximation. Therefore, the slant height of the cone with radius is 0.75 cm. The slant height is the diagonal distance from the top vertex of the cone to the edge of the base.
By just knowing the cone's volume and height, we were able to find its radius, its slant height, and its surface area. More specifically, it's the length of an imaginary line that runs from the center of the circular base to the very tip of the cone. Represents the radius of the circular base of the cone. Before we explain how to use our surface area of a cone calculator, let's first define what type of cone you can use it on.
A generic cone shape consists of a circular or oval base and a vertex above the base connected to the perimeter of the base shape. Is it possible for a pyramid to have altitude greater than slant height? Finally, we need to know the length of YM to have enough information to solve this problem. We were given that the sides of the base of the pyramid measure 12 inches, so we had labeled RA with that measurement. YM is half the length of a side because M is in the middle of the square base.
To calculate the length of the slant height, we need to find the right triangle inside the pyramid. That triangle is made up of points D, M, and Y. Let's draw and label the lengths of its sides.
Now, we draw in the altitude of the cone from A straight down to BC, so that a right angle is created. Point M is the point where the altitude meets BC. Triangle AMC is a right triangle where AM is the altitude and AC is the slant height of the original cone.
AC is also the hypotenuse of the right triangle, since it is the side opposite the right angle. If you drop a yardstick straight down through the hole in the top of the cone until it hits the bottom, that measurement is the altitude. The yardstick in this case will make a right angle at the center of the base. Take a look at the picture to see these measurements labeled.